Sliding Window Algorithm – Fixed & Variable Size Solutions

The sliding window algorithm is one of the most efficient techniques used in solving problems that involve arrays, strings, or lists. This algorithm is widely used because it reduces the time complexity of many problems, making it an essential tool for programmers. Whether you’re working on problems related to subarrays, substrings, or even dynamic programming, the sliding window algorithm helps to optimize your solution.

In this article, we will take a deep dive into the sliding window algorithm, exploring both fixed-length and variable-length solutions. Through practical examples, we will guide you on how and when to apply this powerful technique.

Table of Contents

What is the Sliding Window Algorithm?

The sliding window algorithm is an optimization technique that efficiently solves problems involving contiguous subarrays or substrings. It eliminates the need to repeatedly compute sums, averages, or other values for overlapping sections of the array, improving performance.

In the sliding window approach, you maintain a subset of elements, known as the window, that moves across the data structure. Rather than recalculating values for the entire window each time, you update it incrementally by removing the element that exits and adding the new element that enters.

This technique is particularly useful when you want to:

Find the maximum or minimum sum of a fixed number of elements.
Count unique elements in a subarray.
Solve problems involving continuous subarrays or substrings.

Also check: Backtracking Algorithm Explained With Examples

Use case for Sliding Window Algorithm

Now that we have some idea about the sliding algorithm, let’s check the scenarios or problems in which it would be useful. Whenever we encounter a scenario where we have to find out the maximum/ largest or minimum/ smallest substring or subarray, we have to check if we can apply the sliding window algorithm in such cases.

Suppose we encounter a problem to find the subarray of size 3 which has the maximum sum.

Another problem could be to find the smallest subarray with a sum greater than k.

The usual or brute force approach would be to have two for loops iterate through the entire array and find the solution. The time complexity for the solution would be O(n²). But we can do better. How? You’ll find out in the later sections.

Types of Sliding Window Approaches

1. Fixed Size Sliding Window

In the fixed-size sliding window, the size of the window remains constant throughout the problem. The window slides over the data one by one element at a time, and the operation is performed on the elements inside the window.

This approach is typically used when you know the exact size of the subarray or substring you need to work with.

Steps for Fixed-Size Sliding Window

Step 1: Initialize the window

We first initialize the window with the window size. If the window is 3, the current window will contain elements at index 0, 1, & 2.

Step 2: Slide the window

Now, we slide the window by one element at a time. For each new window, we subtract the element that is left behind and add the new element to the window. Keep doing this till you reach the end of the array.

Step 3: Find the result

While sliding the window, always compare the current window value with the previously calculated window values to get the result.

Example: Maximum Sum of Subarray of Size K

Problem: Given an array, find the maximum sum of any subarray of size K.

Input:
Array: [2, 2, 1, 5, 3, 0]
Window size (k): 3

Step-by-Step Solution: The goal is to find the maximum sum of any subarray that contains exactly 3 consecutive elements.

1. Window Size 3: [2, 2, 1] → Sum = 2 + 2 + 1 = 5

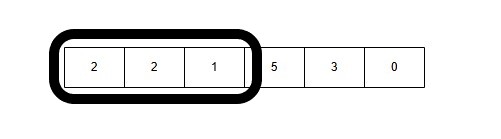
2. Window Size 3: [2, 1, 5] → Sum = 2 + 1 + 5 = 8

3: Window Size 3: [1, 5, 3] → Sum = 1 + 5 + 3 = 9

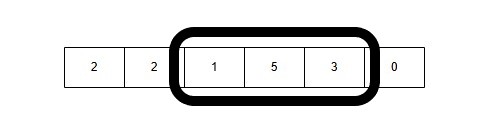
4: Window Size 3: [5, 3, 0] → Sum = 5 + 3 + 0 = 8

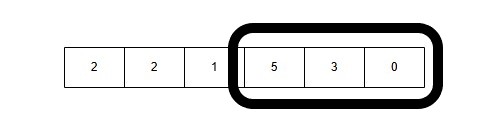
So the maximum sum among these windows is 9.

Final Answer: The maximum sum of any subarray of size 3 is 9.

For the above example, here’s a visual representation of how the fixed-size sliding window algorithm works. Click the arrows to view the steps or you can use the “Auto Play” button to view the full visualisation in one go.

Time Complexity:
The time complexity of this approach is O(n), where n represents the length of the array. First, we compute the sum of the initial k elements. Then, for each subsequent window, we update the sum in constant time, making the process highly efficient.

2. Variable-Size Sliding Window

In the variable-size sliding window algorithm, the window size is not fixed. Instead, the window grows or shrinks based on specific conditions (such as achieving a sum greater than a target value). This approach is often used when the problem requires finding the smallest or largest subarray that meets a given condition.

Steps for Variable-Size Sliding Window

Step 1: Initialize the window

We initialize the window by adding elements to the window as long as the criteria are satisfied. If we have to talk about the criterion, it can be a value less than, greater than, or equal to a value, or something entirely different. It entirely depends on the problem statement at hand.

Step 2: Shrink the window

Once we breach the condition, we reduce or shrink the window. We continue reducing the window until we satisfy the criteria. The criterion can be a value less than, greater than, or equal to a value, or something entirely different. It entirely depends on the problem statement at hand.

Step 3: Find the result

While shrinking/ increasing the window, the important thing to note is that we need to calculate the result at every step. We do this because we can get the result at any and every step.

Example: Smallest Subarray with Sum Greater Than S

Problem: Find the smallest subarray whose sum is greater than a given value S.

Input:
Array: [2, 2, 1, 5, 3, 0]
Target sum (S): 7

Step-by-Step Solution: We need to find the smallest subarray whose sum is greater than 7.

1: Window Size 1: [2] → Sum = 2

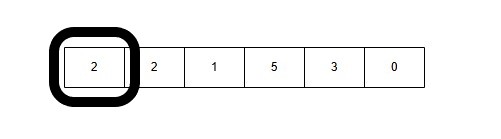
2: Window Size 2: [2, 2] → Sum = 2 + 2 = 4

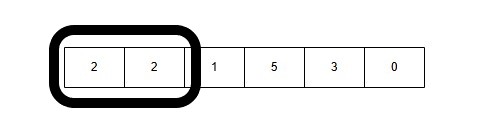
3: Window Size 3: [2, 2, 1] → Sum = 2 + 2 + 1 = 5

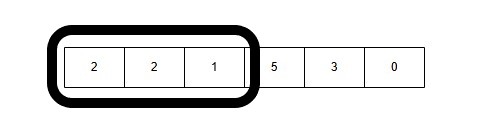
4: Window Size 4: [2, 2, 1, 5] → Sum = 2 + 2 + 1 + 5 = 10(Sum > 7)

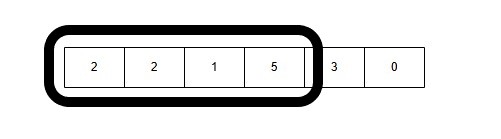
5: Window Size 3: [2, 1, 5] → Sum = 2 + 1 + 5 = 8(Sum > 7)

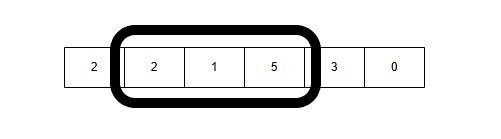
6: Window Size 2: [1, 5] → Sum = 1 + 5 = 6

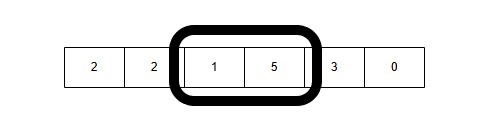
7: Window Size 3: [1, 5, 3] → Sum = 1 + 5 + 3 = 9(Sum > 7)

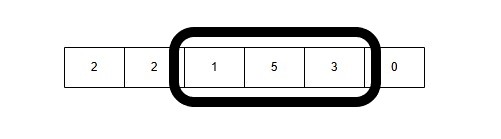
8: Window Size 2: [5, 3] → Sum = 5 + 3 = 8(Sum > 7)

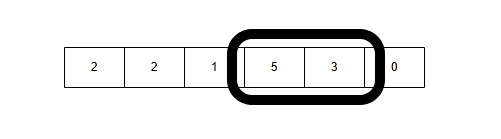
9: Window Size 3: [5, 3, 0] → Sum = 5 + 3 + 0 = 8(Sum > 7)

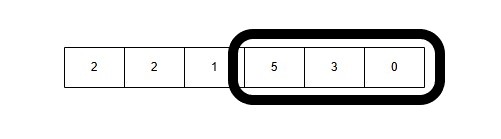
10: Window Size 2: [3, 0] → Sum = 3 + 0 = 3

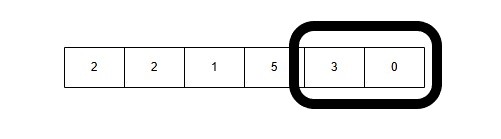
11: Window Size 1: [0] → Sum = 0

As seen above, the subarray [2, 2, 1, 5] is the first valid subarray whose sum is greater than 7, but it is not the smallest. We continued to expand and shrink the window to find the smallest valid subarray.

Final Answer: The smallest subarray with a sum greater than 7 is [5, 3] with a sum of 8.

For the above example, here’s a visual representation of how the variable-size sliding window algorithm works. Click the arrows to view the steps or you can use the “Auto Play” button to view the full visualisation in one go.

Time Complexity:
The time complexity of this approach is O(n), where n is the array’s length. Each element is added and removed from the window at most once, so the total number of operations is proportional to the size of the array.

Also check: Greedy Algorithm: A Comprehensive Guide With Examples

Advantages of the Sliding Window Algorithm

Efficient: The sliding window technique is highly efficient for problems involving contiguous subarrays or substrings, especially when dealing with large input sizes. By incrementally updating the window, you avoid recalculating values from scratch.
Optimal Time Complexity: The sliding window approach reduces the time complexity from O(n^2) (in the case of brute-force solutions) to O(n) in many problems.
Memory Efficient: In some cases, the sliding window can also help reduce memory usage since we only need to keep track of a small subset of the array at any given time.

Common Applications of the Sliding Window Algorithm

The sliding window algorithm has a wide range of applications, especially in array and string manipulation problems. Some common problems where this algorithm is useful include:

Finding the Maximum or Minimum Sum of a Subarray: As demonstrated in the fixed-length sliding window example.
Longest Substring with Unique Characters: You can use a sliding window to find the longest substring of unique characters in a given string.
Finding Subarrays with a Given Sum: The sliding window technique can help find subarrays that meet certain sum criteria.
Dynamic Programming: Sliding windows are used to optimize the calculations of subproblems in some dynamic programming problems.

Important Problems Based on The Sliding Window Algorithm

There are a lot of problems that can be solved using the sliding window algorithm. Some important problems based on the sliding window algorithm are mentioned below. The names of the companies where these questions were asked are included in brackets.

Find All Anagrams in a String (PayTM, Barclays, HCL Technologies, Western Digital, Wipro)
Find K Closest Elements (PayPal, Flipkart, Morgan Stanley, Oyo)
Longest Substring Without Repeating Characters (BrowserStack, Cisco, Samsung)
Minimum Size Subarray Sum (ThoughtWorks, VMware, Myntra)
Sliding Window Maximum (Adobe, Oracle, Apple, EPAM Systems, Virtusa)
Repeated DNA Sequences (eBay, Bank of America)

Conclusion

The sliding window algorithm is a powerful technique that allows you to solve problems involving subarrays or substrings efficiently. By maintaining a window of elements and sliding it over the data, you can calculate solutions in O(n) time, which is much more efficient than brute-force methods.

In this guide, we’ve covered both fixed-length and variable-length sliding window solutions, provided practical examples, and explained the time complexities involved. Whether you’re working on a coding interview question or solving a real-world problem, understanding the sliding window algorithm will make you a more efficient problem solver.

That’s all on the sliding window algorithm.

To keep yourself up to date with our latest content, please subscribe to our newsletter by dropping your email address here: Signup for Our Newsletter.

Please follow us on Medium.