Blog

Median of Two Sorted Arrays Leetcode Problem – 5 Solutions in Java: Naive, Intermediate, Optimal, and More

The median of two sorted arrays problem is a foundational question that showcases your grasp of searching algorithms, edge-case handling, and performance tuning. It often appears in technical interviews because it challenges candidates to balance clarity, efficiency, and correctness. This article explores this problem in Java, starting from a simple brute force method and incrementally moving to the optimal binary search approach. We’ll explain each step with detailed reasoning, examples, and Java code that’s fully commented.

Problem Statement

Leetcode Problem: Median of Two Sorted Arrays

Given two sorted arrays nums1 and nums2 of size m and n, respectively, find the median of the two sorted arrays. The combined runtime complexity should ideally be O(log(min(m,n))).

The median is the value separating the higher half from the lower half of a data sample. If the combined length is even, it’s the average of the two middle numbers.

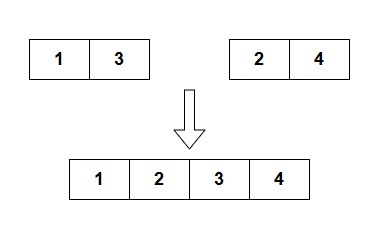
Median of Two Sorted Arrays

Brute Force Approach For Median of Two Sorted Arrays – Merge and Sort

Idea

The most straightforward way is to merge both arrays and sort them. Once we have a sorted combined array, finding the median becomes trivial.

Example

Let’s say:

nums1 = [1, 3]
nums2 = [2, 4]

Merged and sorted array: [1, 2, 3, 4]. Median = (2 + 3) / 2 = 2.5

Brute Force Median of Two Sorted Arrays – Leetcode Solution

import java.util.*;

public class MedianOfTwoSortedArrays {
    public static double findMedianBruteForce(int[] nums1, int[] nums2) {
        int[] merged = new int[nums1.length + nums2.length];
        int index = 0;

        for (int num : nums1) merged[index++] = num;
        for (int num : nums2) merged[index++] = num;

        Arrays.sort(merged); // Sorting the merged array

        int mid = merged.length / 2;
        if (merged.length % 2 == 0) {
            return (merged[mid - 1] + merged[mid]) / 2.0;
        } else {
            return merged[mid];
        }
    }
}

Complexity

  • Time: O((m+n) log(m+n)) due to sorting
  • Space: O(m+n)

Verdict

Simple and effective for small arrays, but inefficient for large inputs due to sorting.

Also check: Palindrome Number Leetcode Problem – 5 Solutions in Java: Naive, Intermediate, Optimal, and More

Median of Two Sorted Arrays – Intermediate Solution – Merge While Finding Median (Two Pointers)

Idea

We don’t need the entire merged array—just the middle values. By using two pointers to simulate merging, we can track the needed values on the fly.

Explanation

You traverse both arrays until you reach the median index. At each step, advance the pointer pointing to the smaller element.

Intermediate Median of Two Sorted Arrays – Leetcode Solution

public static double findMedianTwoPointers(int[] nums1, int[] nums2) {
    int m = nums1.length, n = nums2.length;
    int totalLength = m + n;
    int medianIndex1 = (totalLength - 1) / 2;
    int medianIndex2 = totalLength / 2;

    int i = 0, j = 0, count = 0;
    int prev = 0, curr = 0;

    while (count <= medianIndex2) {
        prev = curr;

        if (i < m && (j >= n || nums1[i] < nums2[j])) {
            curr = nums1[i++];
        } else {
            curr = nums2[j++];
        }
        count++;
    }

    if (totalLength % 2 == 0) {
        return (prev + curr) / 2.0;
    } else {
        return curr;
    }
}

Complexity

  • Time: O(m + n) in worst case
  • Space: O(1)

Verdict

More efficient than brute force, especially for partially overlapping arrays.

Median of Two Sorted Arrays – Intermediate Solution – Simulated Merge with Skipped Elements

Idea

This approach simulates the merging process but skips unnecessary parts. We count elements without storing them, stopping once we reach the median positions.

Optimization

You don’t need to build a full array. Just keep track of elements at positions (m+n)/2 and (m+n-1)/2.

Intermediate Median of Two Sorted Arrays – Leetcode Solution

public static double findMedianSimulatedMerge(int[] nums1, int[] nums2) {
    int m = nums1.length, n = nums2.length;
    int totalLength = m + n;
    int medianIndex1 = (totalLength - 1) / 2;
    int medianIndex2 = totalLength / 2;

    int i = 0, j = 0;
    int count = 0;
    int prev = 0, curr = 0;

    while (count <= medianIndex2) {
        prev = curr;
        if (i < m && (j >= n || nums1[i] < nums2[j])) {
            curr = nums1[i++];
        } else {
            curr = nums2[j++];
        }
        count++;
    }

    if (totalLength % 2 == 0) {
        return (prev + curr) / 2.0;
    } else {
        return curr;
    }
}

Complexity

  • Time: O(m + n)
  • Space: O(1)

Verdict

Intermediate solution that is simple and efficient in practice, though still linear in time.

Also check: How to Prepare for and Crack the Coding Interview

Median of Two Sorted Arrays – Intermediate Solution – Find K-th Element Using Binary Search

Idea

To find the median, you essentially want the (m+n)/2-th smallest element. You can do this by eliminating k/2 elements at each step, similar to binary search.

Key Insight

At every step, compare the k/2-th element from both arrays. Discard the half that cannot contain the k-th element.

Intermediate Median of Two Sorted Arrays – Leetcode Solution

public static double findMedianKthElement(int[] nums1, int[] nums2) {
    int total = nums1.length + nums2.length;
    if (total % 2 == 1) {
        return findKth(nums1, nums2, total / 2 + 1);
    } else {
        return (findKth(nums1, nums2, total / 2) + findKth(nums1, nums2, total / 2 + 1)) / 2.0;
    }
}

private static int findKth(int[] A, int[] B, int k) {
    int m = A.length, n = B.length;
    int i = 0, j = 0;

    while (true) {
        if (i == m) return B[j + k - 1];
        if (j == n) return A[i + k - 1];
        if (k == 1) return Math.min(A[i], B[j]);

        int half = k / 2;
        int newI = Math.min(i + half, m) - 1;
        int newJ = Math.min(j + half, n) - 1;

        if (A[newI] <= B[newJ]) {
            k -= (newI - i + 1);
            i = newI + 1;
        } else {
            k -= (newJ - j + 1);
            j = newJ + 1;
        }
    }
}

Complexity

  • Time: O(log(k)) ~ O(log(m + n))
  • Space: O(1)

Verdict

A clever and effective divide-and-conquer method, suitable for larger arrays.

Median of Two Sorted Arrays – Optimal Solution – Binary Search on Partition

Idea

This method partitions the arrays such that all elements in the left part are less than or equal to those in the right part. It uses binary search on the smaller array.

Key Concepts

  • Total number of elements on the left and right must be equal (or off by 1)
  • Ensure: max(left) <= min(right) for both arrays

Optimal Median of Two Sorted Arrays – Leetcode Solution

public static double findMedianBinarySearch(int[] nums1, int[] nums2) {
    if (nums1.length > nums2.length) {
        return findMedianBinarySearch(nums2, nums1);
    }

    int x = nums1.length;
    int y = nums2.length;
    int low = 0, high = x;

    while (low <= high) {
        int partitionX = (low + high) / 2;
        int partitionY = (x + y + 1) / 2 - partitionX;

        int maxLeftX = (partitionX == 0) ? Integer.MIN_VALUE : nums1[partitionX - 1];
        int minRightX = (partitionX == x) ? Integer.MAX_VALUE : nums1[partitionX];

        int maxLeftY = (partitionY == 0) ? Integer.MIN_VALUE : nums2[partitionY - 1];
        int minRightY = (partitionY == y) ? Integer.MAX_VALUE : nums2[partitionY];

        if (maxLeftX <= minRightY && maxLeftY <= minRightX) {
            if ((x + y) % 2 == 0) {
                return (Math.max(maxLeftX, maxLeftY) + Math.min(minRightX, minRightY)) / 2.0;
            } else {
                return Math.max(maxLeftX, maxLeftY);
            }
        } else if (maxLeftX > minRightY) {
            high = partitionX - 1;
        } else {
            low = partitionX + 1;
        }
    }

    throw new IllegalArgumentException("Input arrays are not sorted");
}

Complexity

  • Time: O(log(min(m, n)))
  • Space: O(1)

Verdict

This is the most optimal and elegant solution, meeting all time and space requirements for the problem.

Conclusion

Solving the median of two sorted arrays problem provides valuable insight into algorithmic thinking and optimization. Whether you start with the brute force solution or implement the elegant binary search partition, each method teaches a new layer of logic and performance refinement.

In real-world applications—like data stream analysis, sensor data aggregation, or merging logs—these techniques can scale well and maintain performance. Mastering this problem helps sharpen your skills for more complex algorithmic challenges.

That’s all on the Median of Two Sorted Arrays Java Leetcode solutions.

To keep yourself up to date with our latest content, please subscribe to our newsletter by dropping your email address here: Signup for Our Newsletter.

Please follow us on Medium.

Further Reading